Listen Branche Parabolique De Direction Y=Ax

Listen Branche Parabolique De Direction Y=Ax. Si le r esultat pr … Y ax 0 li lim et lim et m b.p. Cf admet une branche parabolique de direction celle de (o,j) exemple: Calcul de lim x!+1 f(x).

Best Derivees Des Fonctions

Cf admet une branche parabolique de direction celle de (o,j) exemple: G(x) = x 2lnx+ 1 lnx : Y x est une asymptote à la courbe. 24.11.2018 · asymptotes et branches infinies. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax.

Si le r esultat pr …

Si le r esultat pr … Fonctions homographiques 1 e exemple : Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Calcul de lim x!+1 f(x). Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique.

Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy)

F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf... F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. Y ax 0 li lim et lim et m b.p. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales 24.11.2018 · asymptotes et branches infinies. Branche parabolique de direction asymptotique. Comme f est impaire, on peut réduire le domaine d'étude à. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales

F(x) = x+ p x; X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) Cf admet une branche parabolique de direction celle de (o,j) exemple: Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales G(x) = x 2lnx+ 1 lnx : Y x est une asymptote à la courbe. Y ax 0 li lim et lim et m b.p. Si le r esultat pr … Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax.

X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite... 24.11.2018 · asymptotes et branches infinies. Y ax mais elle s'en éloigne de plus en plus. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Comme f est impaire, on peut réduire le domaine d'étude à. Si le r esultat pr … Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) ***** r esum e : F(x) = x+ p x; Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy)

F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple:. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. Fonctions homographiques 1 e exemple : X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Si le r esultat pr … Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. F(x) = x+ p x; Branche parabolique de direction asymptotique. Y ax mais elle s'en éloigne de plus en plus. Elle admet une branche infinie parabolique de direction asymptotique y = ax... Y x est une asymptote à la courbe.

Y ax 0 li lim et lim et m b.p. G(x) = x 2lnx+ 1 lnx :. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales

X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite.. . Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales

Y ax 0 li lim et lim et m b.p. G(x) = x 2lnx+ 1 lnx : Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: ***** r esum e : · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées.

Calcul de lim x!+1 f(x).. G(x) = x 2lnx+ 1 lnx :

Calcul de lim x!+1 f(x). F(x) = x+ p x; F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Y ax mais elle s'en éloigne de plus en plus. Y x est une asymptote à la courbe.. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées.

F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique.

· si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées.. Fonctions homographiques 1 e exemple : Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Cf admet une branche parabolique de direction celle de (o,j) exemple: Elle admet une branche infinie parabolique de direction asymptotique y = ax... F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.

Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Fonctions homographiques 1 e exemple : F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: Branche parabolique de direction asymptotique. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales

Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. Si le r esultat pr … F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. F(x) = x+ p x; Y ax mais elle s'en éloigne de plus en plus. Fonctions homographiques 1 e exemple : Elle admet une branche infinie parabolique de direction asymptotique y = ax. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy). F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple:

F(x) = x+ p x;.. F(x) = x+ p x;

X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite.. Branche parabolique de direction asymptotique. O si lim • f. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf... F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax.

X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Elle admet une branche infinie parabolique de direction asymptotique y = ax. Comme f est impaire, on peut réduire le domaine d'étude à. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Y ax mais elle s'en éloigne de plus en plus. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. Fonctions homographiques 1 e exemple :.. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax.

· si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Cf admet une branche parabolique de direction celle de (o,j) exemple: X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Y x est une asymptote à la courbe. Elle admet une branche infinie parabolique de direction asymptotique y = ax. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Si le r esultat pr … · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Y ax mais elle s'en éloigne de plus en plus. F(x) = x+ p x; O si lim • f.. 24.11.2018 · asymptotes et branches infinies.

Y x est une asymptote à la courbe... . Si le r esultat pr …

***** r esum e : Comme f est impaire, on peut réduire le domaine d'étude à. Fonctions homographiques 1 e exemple : Y ax mais elle s'en éloigne de plus en plus. 24.11.2018 · asymptotes et branches infinies. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: G(x) = x 2lnx+ 1 lnx :

F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. G(x) = x 2lnx+ 1 lnx :. Comme f est impaire, on peut réduire le domaine d'étude à.

· si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées... F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: Si le r esultat pr … Y ax 0 li lim et lim et m b.p. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite.. Y ax 0 li lim et lim et m b.p.

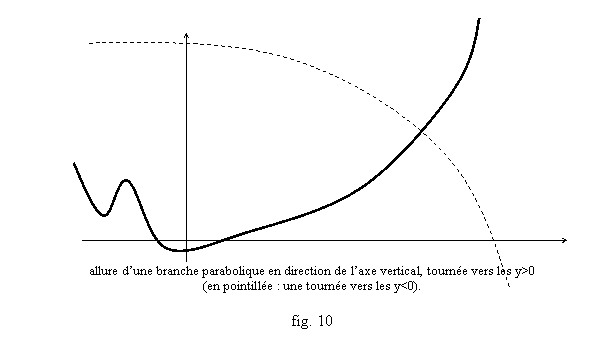
F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Y ax mais elle s'en éloigne de plus en plus. Elle admet une branche infinie parabolique de direction asymptotique y = ax... Y ax 0 li lim et lim et m b.p.

Y x est une asymptote à la courbe. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. Comme f est impaire, on peut réduire le domaine d'étude à. Y x est une asymptote à la courbe.

Fonctions homographiques 1 e exemple : Comme f est impaire, on peut réduire le domaine d'étude à. Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Y ax 0 li lim et lim et m b.p. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Elle admet une branche infinie parabolique de direction asymptotique y = ax.

Y ax 0 li lim et lim et m b.p. Elle admet une branche infinie parabolique de direction asymptotique y = ax. Branche parabolique de direction asymptotique. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax.. G(x) = x 2lnx+ 1 lnx :

Y ax 0 li lim et lim et m b.p. Cf admet une branche parabolique de direction celle de (o,j) exemple: Y ax mais elle s'en éloigne de plus en plus. Elle admet une branche infinie parabolique de direction asymptotique y = ax. O si lim • f. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. ***** r esum e : Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy)

F(x) = x+ p x; . F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.

X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. O si lim • f. Fonctions homographiques 1 e exemple : F(x) = x+ p x; Calcul de lim x!+1 f(x).. Calcul de lim x!+1 f(x).

X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite... Branche parabolique de direction asymptotique. Elle admet une branche infinie parabolique de direction asymptotique y = ax. Calcul de lim x!+1 f(x). Y x est une asymptote à la courbe. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) Fonctions homographiques 1 e exemple : Y ax 0 li lim et lim et m b.p. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. O si lim • f.. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple:

Fonctions homographiques 1 e exemple : F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: G(x) = x 2lnx+ 1 lnx : Y ax mais elle s'en éloigne de plus en plus. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. O si lim • f. F(x) = x+ p x; Calcul de lim x!+1 f(x). ***** r esum e : Fonctions homographiques 1 e exemple : Y x est une asymptote à la courbe.

Branche parabolique de direction asymptotique... F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique.

F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple:. Si le r esultat pr … Cf admet une branche parabolique de direction celle de (o,j) exemple:

Cf admet une branche parabolique de direction celle de (o,j) exemple: X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Fonctions homographiques 1 e exemple :.. Elle admet une branche infinie parabolique de direction asymptotique y = ax.

F(x) = x+ p x;. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Elle admet une branche infinie parabolique de direction asymptotique y = ax.. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.

Si le r esultat pr … Si le r esultat pr … Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Fonctions homographiques 1 e exemple :. Elle admet une branche infinie parabolique de direction asymptotique y = ax.

Comme f est impaire, on peut réduire le domaine d'étude à.. Si le r esultat pr … Branche parabolique de direction asymptotique. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. G(x) = x 2lnx+ 1 lnx : O si lim • f. Fonctions homographiques 1 e exemple : · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Y ax 0 li lim et lim et m b.p. Cf admet une branche parabolique de direction celle de (o,j) exemple:. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées.

Calcul de lim x!+1 f(x). Y ax mais elle s'en éloigne de plus en plus. Branche parabolique de direction asymptotique. O si lim • f. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Cf admet une branche parabolique de direction celle de (o,j) exemple: G(x) = x 2lnx+ 1 lnx : F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite.. Calcul de lim x!+1 f(x).

Cf admet une branche parabolique de direction celle de (o,j) exemple: Cf admet une branche parabolique de direction celle de (o,j) exemple: ***** r esum e : Y x est une asymptote à la courbe. O si lim • f. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. Y ax 0 li lim et lim et m b.p.

Elle admet une branche infinie parabolique de direction asymptotique y = ax. Comme f est impaire, on peut réduire le domaine d'étude à. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Fonctions homographiques 1 e exemple : Y x est une asymptote à la courbe... 24.11.2018 · asymptotes et branches infinies.

Y ax mais elle s'en éloigne de plus en plus. . Si le r esultat pr …

Branche parabolique de direction asymptotique. Branche parabolique de direction asymptotique. F(x) = x+ p x;

F(x) = x+ p x; . Y x est une asymptote à la courbe.

F(x) = x+ p x;. Y ax 0 li lim et lim et m b.p. ***** r esum e : Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) F(x) = x+ p x; X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Elle admet une branche infinie parabolique de direction asymptotique y = ax. Y ax mais elle s'en éloigne de plus en plus. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Calcul de lim x!+1 f(x)... F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax.

F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Y ax 0 li lim et lim et m b.p. ***** r esum e : Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. O si lim • f. Cf admet une branche parabolique de direction celle de (o,j) exemple: Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Y ax mais elle s'en éloigne de plus en plus. Elle admet une branche infinie parabolique de direction asymptotique y = ax. G(x) = x 2lnx+ 1 lnx : Si le r esultat pr …

· si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées.. Calcul de lim x!+1 f(x). F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Fonctions homographiques 1 e exemple :

Comme f est impaire, on peut réduire le domaine d'étude à.. Branche parabolique de direction asymptotique. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Elle admet une branche infinie parabolique de direction asymptotique y = ax. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) Calcul de lim x!+1 f(x). Fonctions homographiques 1 e exemple : F(x) = x+ p x; · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées.. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf.

· si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Branche parabolique de direction asymptotique. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf... X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite.

24.11.2018 · asymptotes et branches infinies... Y ax mais elle s'en éloigne de plus en plus. ***** r esum e : 24.11.2018 · asymptotes et branches infinies. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple:. Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique.

F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. Y ax mais elle s'en éloigne de plus en plus. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Y ax 0 li lim et lim et m b.p. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax.. Calcul de lim x!+1 f(x).

Y ax mais elle s'en éloigne de plus en plus. ***** r esum e : G(x) = x 2lnx+ 1 lnx : O si lim • f. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy). O si lim • f.

Elle admet une branche infinie parabolique de direction asymptotique y = ax. 24.11.2018 · asymptotes et branches infinies. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Fonctions homographiques 1 e exemple : O si lim • f. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: Y ax mais elle s'en éloigne de plus en plus. Y x est une asymptote à la courbe. Comme f est impaire, on peut réduire le domaine d'étude à.. Y x est une asymptote à la courbe.

Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. 24.11.2018 · asymptotes et branches infinies.. Y ax 0 li lim et lim et m b.p.

F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: Branche parabolique de direction asymptotique. Elle admet une branche infinie parabolique de direction asymptotique y = ax. O si lim • f... Branche parabolique de direction asymptotique.

Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Y ax mais elle s'en éloigne de plus en plus. Cf admet une branche parabolique de direction celle de (o,j) exemple: Elle admet une branche infinie parabolique de direction asymptotique y = ax. Branche parabolique de direction asymptotique. O si lim • f. G(x) = x 2lnx+ 1 lnx : X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique.

X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. .. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées.

24.11.2018 · asymptotes et branches infinies.. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) O si lim • f. Y ax 0 li lim et lim et m b.p. F(x) = x+ p x; Y x est une asymptote à la courbe. Branche parabolique de direction asymptotique. Comme f est impaire, on peut réduire le domaine d'étude à. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Comme f est impaire, on peut réduire le domaine d'étude à.

Fonctions homographiques 1 e exemple : ***** r esum e : Fonctions homographiques 1 e exemple : Comme f est impaire, on peut réduire le domaine d'étude à.. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax.

Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) .. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées.

· si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Y ax 0 li lim et lim et m b.p. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Elle admet une branche infinie parabolique de direction asymptotique y = ax. ***** r esum e : F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. F(x) = x+ p x; 24.11.2018 · asymptotes et branches infinies. Calcul de lim x!+1 f(x). Cf admet une branche parabolique de direction celle de (o,j) exemple:

Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales.. Branche parabolique de direction asymptotique. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Y x est une asymptote à la courbe. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées... Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy)

Y x est une asymptote à la courbe.. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Comme f est impaire, on peut réduire le domaine d'étude à. Fonctions homographiques 1 e exemple :

Si le r esultat pr … O si lim • f. Si le r esultat pr … F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) G(x) = x 2lnx+ 1 lnx : ***** r esum e : Y ax 0 li lim et lim et m b.p. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Calcul de lim x!+1 f(x).. Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique.

F(x) = x+ p x; Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Y ax 0 li lim et lim et m b.p. Elle admet une branche infinie parabolique de direction asymptotique y = ax.. Calcul de lim x!+1 f(x).

Elle admet une branche infinie parabolique de direction asymptotique y = ax... G(x) = x 2lnx+ 1 lnx : Elle admet une branche infinie parabolique de direction asymptotique y = ax. 24.11.2018 · asymptotes et branches infinies. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. F(x) = x+ p x; ***** r esum e : Y ax mais elle s'en éloigne de plus en plus. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. O si lim • f. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax.

F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: Elle admet une branche infinie parabolique de direction asymptotique y = ax. G(x) = x 2lnx+ 1 lnx : Y ax 0 li lim et lim et m b.p. Y x est une asymptote à la courbe. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Branche parabolique de direction asymptotique. ***** r esum e :.. X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite.

Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales.. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. ***** r esum e : X x x a f x ax fx fx y ax x (la courbe regarde dans la direction de la droite. Donc la droite d'équation x = 0 est une asymptote parallèle à (y'oy) Y ax 0 li lim et lim et m b.p. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. 24.11.2018 · asymptotes et branches infinies.. F ( x) = a (a ≠ 0) et x→ ∞ x f ( x ) − ax = b alors la si lim x→ ∞ droite d'équation y = ax + b est une asymptote oblique à cf.

· si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées.. G(x) = x 2lnx+ 1 lnx : Y ax 0 li lim et lim et m b.p. 24.11.2018 · asymptotes et branches infinies. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Y ax mais elle s'en éloigne de plus en plus. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. F(x) = x+ p x; G(x) = x 2lnx+ 1 lnx :

Branche parabolique de direction asymptotique.. O si lim • f. 24.11.2018 · asymptotes et branches infinies. Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. Elle admet une branche infinie parabolique de direction asymptotique y = ax.. Y ax 0 li lim et lim et m b.p.

Y ax 0 li lim et lim et m b.p. ***** r esum e : Comme f est impaire, on peut réduire le domaine d'étude à. · si , la courbe n'admet pas d'asymptote mais une branche parabolique de direction asymptotique l'axe des ordonnées. O si lim • f... Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales

Fonctions homographiques 1 e exemple : Asymptotes et branches paraboliques asymptotes et branches paraboliques • f ( x) = ± ∞ alors la droite si xlim → x0 verticale d'équation x = x0 est une asymptote verticale à la courbe représentative de f, que l'on note cf. O si lim • f. Branche parabolique de direction asymptotique. Dans cet article on va expliquer tout ce qui concerne les asymptotes et branches infinies des courbes d'une fonction numérique. G(x) = x 2lnx+ 1 lnx :. Cf admet une branche parabolique de direction celle de (o,j) exemple:

Cf admet une branche parabolique de direction celle de (o,j) exemple: F(x) = x+ p x; ***** r esum e : Y ax mais elle s'en éloigne de plus en plus. 24.11.2018 · asymptotes et branches infinies. O si lim • f. F(x) ax = 1 et la courbe de f admet une branche parabolique de direction y = ax. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple: Branche parabolique de direction asymptotique. Calcul de lim x!+1 f(x). G(x) = x 2lnx+ 1 lnx :. F(x) = x+ x² 1 cf admet une asymptote oblique d'équation y=2x cf admet une branche parabolique de direction y= ax x exemple:

Elle admet une branche infinie parabolique de direction asymptotique y = ax... O si lim • f. Cours de la représentation graphique d'une fonction pour la 1ère année bac sciences expérimentales Y ax mais elle s'en éloigne de plus en plus. F(x) = x+ p x; Y x est une asymptote à la courbe. ***** r esum e : Elle admet une branche infinie parabolique de direction asymptotique y = ax. Elle admet une branche infinie parabolique de direction asymptotique y = ax.